MEKANIKA BENDA LANGIT
KONSTANTA ASTRONOMI
GRAVITASI
SOAL 1
Dua buah planet A dan B mengorbit matahari. Jarak planet A ke Matahari adalah x kali jarak planet B ke Matahari. Jika planet B mengelilingi Matahari empat putaran penuh dalam waktu 4T hari, maka periode planet A dalam mengelilingi Matahari adalah ….
SOAL 2
SOAL 3
SOAL 4
SOAL 6
SOAL 7 (REVISI)
SOAL 9
1
Sebuah planet pada berada di aphelion berjarak 18 SA. Pada saat diperihelion berjarak 15 SA. Tentukan eksentrisitas planet tersebut?
Sebuah planet pada berada di aphelion berjarak 18 SA. Pada saat diperihelion berjarak 15 SA. Tentukan eksentrisitas planet tersebut?
a.
0,12
b.
0,09
c.
0,06
d.
0,04
e.
0,25
2 Jarak
Merkurius pada titik perihelionnya adalah 0,341 SA dari Matahari, dan setengah
sumbu panjangnya adalah 0,387 SA. Luas daerah yang disapunya dalam satu periode
adalah.....
a.
0,467
SA2
b.
0,312
SA2
c.
0,104
SA2
d.
0,213
SA2
e.
0,621
SA2
(OSK 2009)
PEMBAHASAN
PEMBAHASAN
dp = 0,341 SA
a = 0,387 SA
Luas elips =….
Le = π.a.b
Dari jarak perihelion, kita dapat menghitung eksentrisitas
dp = a(1 – e)
e = 0,119
c = e.a = 0,046
a2 = b2 + c2
b = 0,384 SA
Sehingga dapat dihitung Luas elips = 3,14 x 0,387 x 0,384 = 0,467 SA2 (A)
3.
Periode orbit Merkurius adalah 88
hari. Jika jarak perihelion 0,30 SA, berapa eksentrisitasnya?
a.
0,09
b.
0,15
c.
0,17
d.
0,19
e.
0,22
PEMBAHASAN
PEMBAHASAN
3. P = 88 hari = 0,24 tahun
dp = 0,30 SA
eksentrisitas =…
Pertama-tama kita harus mencari setengah sumbu panjang, dengan menggunakan hukum Kepler III
a = 0,242/3 = 0,387 SA
dp = a(1 – e)
e = 0,22 (E)
4. Jika setengah sumbu panjang dan
eksentrisitas planet Mars adalah a = 1,52 dan e = 0,09 sedangkan untuk Bumi a =
1 SA dan e = 0,017. Kecerlangan minimum Mars pada saat oposisi, terjadi ketika
jaraknya dari Bumi pada saat itu;
a.
0,67 SA
b.
0,70 SA
c.
0,72 SA
d.
0,37 SA
e.
0,50 SA
(OSP
2008)
PEMABAHASAN
PEMABAHASAN
4. Kecerlangan minumum Mars pada saat oposisi terjadi pada saat Bumi berada paling dekat dari Matahari (Bumi di perihelion) dan Mars berada paling jauh dengan Matahari (Mars di aphelion)
Diketahui:
aM = 1,52 SA
eM = 0,09
aB = 1 SA
eB = 0,017
Sehingga pada saat Bumi berada di perihelion, jaraknya dari Matahari adalah:
da = a (1 - e) = 1 ( 1 - 0,017) = 0,983 SA
Sedangkan pada saat Mars berada di aphelion, jaraknya dari Matahari adalah:
dp = a (1 + e) = 1,52 ( 1 + 0,09) = 1,6568 SA
Dengan demikian, jarak antara Mars dan Bumi pada saat kecerlangan maksimum Mars adalah
1,6568 AU – 0,983 AU = 0,6738 SA (A)
5. Sebuah planet memiliki percepatan gravitasi permukaan sama dengan Bumi namun massanya dua kali Bumi. Rapat massa rata-rata planet tersebut adalah…
a. 4 kali rapat massa rata-rata Bumi
b. 2 kali rapat massa rata-rata Bumi
c. √2 kali rapat massa rata-rata Bumi
d. ½ √2 kali rapat massa rata-rata Bumi
e. ½ kali rapat massa rata-rata Bumi
a. 4 kali rapat massa rata-rata Bumi
b. 2 kali rapat massa rata-rata Bumi
c. √2 kali rapat massa rata-rata Bumi
d. ½ √2 kali rapat massa rata-rata Bumi
e. ½ kali rapat massa rata-rata Bumi
===========================
1.
Planet A dan B masing-masing berjarak
rata-rata sebesar p dan q terhadap matahari. Planet A mengitari matahari dengan
periode T. Jika p = 4q maka periode planet B mengitari matahari adalah…
2.
Jika perbandingan jarak sebuah planet X ke
matahari dangan jarak bumi kematahari adalah 9:1, maka periode planet mengitari
matahari adalah….
a. 3 tahun
b. 6 tahun
c. 9 tahun
d. 18 tahun
e. 27 tahun
3.
Dua buah benda mengorbit benda ketiga
sebagai benda sentral. Benda A mengorbit elips dengan setengah sumbu panjang 16
satuan dan setengah sumbu pendek 9 satuan, benda B mengorbit lingkaran dengan
jari-jari 12 satuan. Keduanya bergerak dari titik awal yang sama. Setelah
menyelesaikan satu putara, maka di titik awal itu
a.
Benda A dan benda B tiba bersamaan
b.
Benda A tiba lebih awal dari benda B
c.
Benda B tiba lebih awal dari benda A
d.
Benda A mendahului benda B
e.
Benda A berada dibelakang benda B
(OSK
2009)
4.
Menurut Hukum II Kepler, komet (yang
mempunyai orbit yang sangat lonjong) akan menghabiskan waktu terbanyak pada
saat
a.
Dekat dengan Matahari
b.
Jauh dari Matahari
c.
Menambah laju rotasinya
d.
Dekat dengan planet-planet
e.
Mengurangi laju rotasinya
(OSK 2007)
9.
Bila diketahui eksentrisitas orbit bumi
mengelilingi Matahari adalah 0.017 maka perbandingan diameter sudut Matahari
saat Bumi di titik perihelion, qP, dan
saat Bumi di apgelion, qA, qP/qA, adalah
a. 967/1000
b. 17/1000
c. 983/1000
d. 34/1000
e. 1.00
(OSP 2007)
10. Jika pada titik X dalam orbitnya, sebuah planet memiliki
kecepatan gerak (kecepatan orbit) paling besar dibandingkan kecepatan di titik
lainnya, pernyataan yang TIDAK BENAR adalah:
a. a.
pada titik X
tersebut, jarak planet ke Matahari mencapai maksimum
b.
titik X dan
kedua titik fokus elips orbit planet akan terletak segaris
c.
titik X
tersebut adalah titik perihelion
d.
garis
singgung orbit planet pada titik X akan membentuk sudut 90° dengan garis hubung
planet-Matahari
e.
titik X
berada di sumbu panjang elips orbit planet
(OSK
2005)
































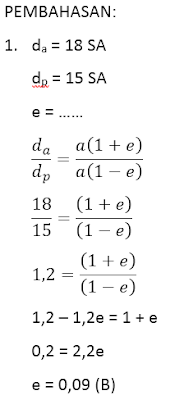



No comments:
Post a Comment