TUGAS PELAJARAN
UNTUK SISWA DARI P WAWAN
HARI RABU, 30
OKTOBER 2019
JAM PELAJARAN KE
|
KELAS
|
TUGAS
|
4
|
X MIPA 5
|
Buka web http://wbsusanto.blogspot.com/
Pelajari materi penguatan Besaran, Satuan, Dimensi, Pengukuran
Kerjakan soal latihan dengan melihat contoh soal
pembahasan
Lembar jawab di kertas tugas diberi identitas nama ,
kelas /no absen, difoto, dan dikirim WA langsung ke P Wawan sebagai bukti
telah mengerjakan setelah itu baru dikumpulkan lembar jawab kertas tersebut
di meja P Wawan di Ruang Guru.
|
5,6
|
XI MIPA 1
|
Buka web http://wbsusanto.blogspot.com/
Pelajari materi ELASTISITAS
Kerjakan soal latihan dengan melihat contoh soal
pembahasan
Lembar jawab di kertas tugas diberi identitas nama ,
kelas /no absen, difoto, dan dikirim WA langsung ke P Wawan sebagai bukti
telah mengerjakan setelah itu baru dikumpulkan lembar jawab kertas tersebut
di meja P Wawan di Ruang Guru.
|
8
|
X MIPA 2
|
Buka web http://wbsusanto.blogspot.com/
Pelajari materi penguatan Besaran, Satuan, Dimensi, Pengukuran
Kerjakan soal latihan dengan melihat contoh soal
pembahasan
Lembar jawab di kertas tugas diberi identitas nama ,
kelas /no absen, difoto, dan dikirim WA langsung ke P Wawan sebagai bukti
telah mengerjakan setelah itu baru dikumpulkan lembar jawab kertas tersebut
di meja P Wawan di Ruang Guru.
|
9,10
|
XII MIPA 3
|
Buka web http://wbsusanto.blogspot.com/
Pelajari materi RELATIVITAS
Kerjakan soal latihan dengan melihat contoh soal
pembahasan
Lembar jawab di kertas tugas diberi identitas nama ,
kelas /no absen, difoto, dan dikirim WA langsung ke P Wawan sebagai bukti
telah mengerjakan setelah itu baru dikumpulkan lembar jawab kertas tersebut
di meja P Wawan di Ruang Guru.
|
Guru Mapel
Wawan Budi Susanto, S.Pd.
TUGAS PELAJARAN KELAS X MIPA
Pelajari materi penguatan Besaran, Satuan, Dimensi, Pengukuran berikut
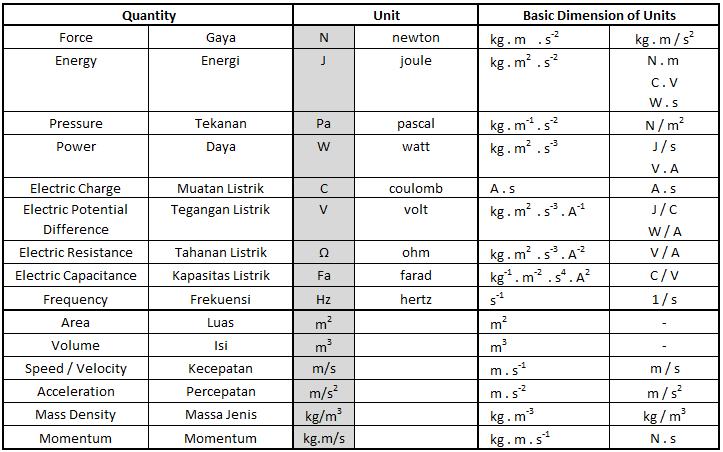
Dimensi adalah satu standar yang dipakai untuk mengidentifikasi dan menentukan besaran (quantity) dari suatu kondisi fisik yang ada, termasuk dalam ilmu konstruksi
Dalam SI (Satuan Internasional) unit terdapat 7 dimensi dasar, dengan kode : mass (M), length (L), time (T), electric current (I), temperature (Θ), amount of substance (N) and intensity of light (J)  |
Dimensi dan Satuan Turunan
Berikut ini beberapa dimensi dan satuan turunan yang banyak digunakan
1. Pengukuran panjang menggunakan jangka sorongBerikut ini beberapa dimensi dan satuan turunan yang banyak digunakan
jangka sorong
Cara Membaca Skala Jangka sorong di atas :
a. Bacalah Skala Utama yang berdekatan dengan angka nol skala nonius. Terbaca antara 2,1 cm dan 2,2 cm
b. Perhatikan skala nonius yang berimpit dengan skala utama. Terlihat skala kelima.
c. Bacaan Jangka sorong :
==> 2,1 cm + 0,05 cm
==> 2,15 cm
2. Pengukuran Panjang menggunakan Mikrometer Sekrup
mikrometer sekrup
Mikrometer sekrup digunakan untuk mengukur panjang maksimal 2,5 cm ( 25 mm ), dengan skala terkecil 0,01 mm.
Cara membaca skala mikrometer sekrup :
a. Bacalah skala utama yang berdekatan dengan tepi selubung luar. Terbaca 4,5 mm dan 5 mm pada gambar.
b. perhatikan skala pada selubung luar yang berimpit dengan garis mendatar skala utama. Terlihat sekala ke 45+2= 47
c. Bacalah Mikrometer sekrup :
==> 4,5 mm + (47 × 0,01) mm
==> 4,5 mm + 0,47 mm
==> 4,97 mm
Cara Menggunakan Neraca Ohaus
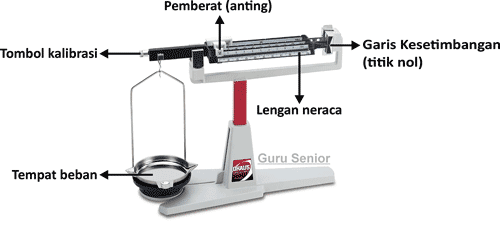
Sebelum kalian dapat menggunakan neraca ohaus dengan benar, kalian perlu memahami bagian-bagian neraca ohaus dan fungsinya terlebih dahulu. Untuk itu silahkan perhatikan gambar di bawah ini.
Fungsi dari kelima bagian neraca ohaus di atas adalah sebagai berikut.
■ Tombol kalibrasi, merupakan sebuah sekrup atau knop yang digunakan untuk mengenolkan atau mengkalibrasi neraca ketika neraca akan digunakan.
■ Tempat beban, merupakan sebuah piringan logam yang digunakan untuk meletakkan benda yang akan diukur massanya.
■ Pemberat (anting), merupakan sebuah logam yang menggantung pada lengan yang berfungsi sebagai penunjuk hasil pengukuran. Pemberat dapat digeser-geser dan setiap lengan neraca memilikinya.
■ Lengan Neraca, merupakan plat logam yang terdiri dari skala dengan ukuran tertentu. Jumlah lengan pada neraca bisa 2, 3 atau 4 bergantung jenisnya. Masing-masing lengan menunjukkan skala dengan satuan yang berbeda.
■ Garis kesetimbangan (titik nol), digunakan untuk menentukan titik kesetimbangan pada proses penimbangan atau pengukuran massa benda.
Adapun langkah-langkah menggunakan neraca ohaus tiga lengan adalah sebagai berikut.
1. Posisikan skala neraca pada posisi nol dengan menggeser pemberat (anting) pada lengan depan, tengah, dan belakang ke sisi kiri dan dan putar tombol kalibrasi sampai garis kesetimbangan mengarah pada angka nol.
2. Periksa bahwa neraca pada posisi setimbang.
3. Letakkan benda yang akan diukur massanya di tempat yang tersedia pada neraca (tempat beban).
4. Geser ketiga pemberat diurutkan dari pemberat yang paling besar ke yang terkecil yaitu dimulai dari lengan yang menunjukkan skala ratusan, puluhan, dan satuan sehingga tercapai keadaan setimbang.
5. Bacalah massa benda dengan menjumlahkan nilai yang ditunjukkan oleh skala ratusan, puluhan, dan satuan atau sepersepuluhan.
Cara Membaca Skala Hasil Pengukuran Neraca Ohaus
Membaca skala alat ukur merupakan langkah terakhir dalam proses pengukuran. Pada neraca ohaus, setelah sistem kesetimbangan tercapai, selanjutnya kalian tinggal membaca skala hasil penimbangan untuk mengetahui berapa massa benda yang ditimbang. Perhatikan contoh soal berikut.
“Sekantong plastik gula pasir ditimbang dengan neraca O’Hauss tiga lengan. Posisi lengan depan, lengan tengah, dan lengan belakang dalam keadaan setimbang ditunjukkan pada gambar di bawah ini. Tentutakanlah massa gula pasir tersebut!”
Jawab:
Berdasarkan gambar di atas, hasil pengukuran menggunakan neraca ohaus adalah sebagai berikut.
Dengan demikian, massa sekantong plastik gula pasir tersebut adalah 542,4 gram.
Berdasarkan jumlah lengannya, neraca ohaus dibagi menjadi 3 jenis, yaitu neraca ohaus 2 lengan, neraca ohaus 3 lengan, dan neraca ohaus 4 lengan. Meski jumlah lengannya berbeda, namun prinsip kerja dan cara penggunaan ketiga jenis neraca ohaus ini tetaplah sama.

Kemudian, setelah tahu jenis-jenisnya, mari kita pahami bagian-bagian neraca ohaus agar Anda tidak bingung mengikuti panduan cara menggunakan neraca ohaus yang akan saya sampaikan nanti.
Sedikitnya ada 5 bagian utama neraca ohaus yang pasti ada dalam setiap jenis-jenis neraca ohaus. Kelima bagian tersebut yaitu:
Nah, setelah tahu apa saja bagian-bagian neraca ohaus, selanjutnya kita bahas bagaimana cara menggunakan neraca ohaus dengan benar.

Kemudian, setelah tahu jenis-jenisnya, mari kita pahami bagian-bagian neraca ohaus agar Anda tidak bingung mengikuti panduan cara menggunakan neraca ohaus yang akan saya sampaikan nanti.
- Tempat beban. Adalah tempat yang digunakan untuk meletakan benda yang hendak diukur.
- Tombol kalibrasi. Adalah sebuah tombol atau knop yang digunakan untuk mengkalibrasi neraca ohaus ketika neraca akan digunakan.
- Lengan neraca. Adalah lengan yang terdiri dari skala dengan ukuran tertentu. jumlah lengan pada neraca bisa 2, 3, atau 4. Masing-masing lengan menunjukan skala dan satuan yang berbeda-beda.
- Pemberat (anting). Adalah sebuah logam yang menggantung pada lengan. Fungsinya sebagai penunjuk hasil pengukuran. Ia dapat digeser-geser dan setiap lengan neraca memilikinya.
- Garis kesetimbangan. Disebut juga Titik 0. Ia digunakan untuk menentukan titik kesetimbangan pada proses penimbangan.
Nah, setelah tahu apa saja bagian-bagian neraca ohaus, selanjutnya kita bahas bagaimana cara menggunakan neraca ohaus dengan benar.
1. Cara Kalibrasi
Sebelum melakukan penimbangan, neraca ohaus terlebih dahulu harus dikalibrasi agar hasil penimbangan nantinya dapat akurat. Untuk melakukan kalibrasi, pertama letakan semua anting pada lengan neraca di titik terendah dari skala yang ditunjukan. Kemudian putar sekrup atau tombol kalibrasi yang letaknya berada di bawah tempat beban. Putar sekrup hingga neraca mencapai garis kesetimbangan (titik 0). Setelah itu, neraca ohaus siap digunakan.
2. Cara Penimbangan
Cara menggunakan neraca ohaus diawali dengan meletakan beban yang ingin diketahui massanya (ditimbang) ke dalam wadah beban. Setelah itu, geser anting pada lengan yang menunjukan skala paling besar sampai garis kesetimbangan hampir tercapai.
Jika garis kesetimbangan belum tercapai, geser anting pada lengan yang menunjukan skala lebih kecil sampai garis kesetimbangan tercapai. Dan jika belum juga, lakukan hal yang sama pada anting di lengan selanjutnya sampai titik kesetimbangan benar-benar tercapai.

Pada gambar di atas, dapat kita lihat bahwa lengan pertama menunjukan skala 400 gram, lengan kedua menunjukan skala 50 gram, dan lengan ketiga menunjukan skala 6,5 gram. Dari skala yang ditunjukan ketiga lengan, kita dapat mengetahui massa benda dengan menjumlahkan semua skala yang ditunjukan masing-masing lengan, yaitu 400 gr + 50 gr + 6,5 gr = 456,5 gr.
Cara menggunakan neraca ohaus diawali dengan meletakan beban yang ingin diketahui massanya (ditimbang) ke dalam wadah beban. Setelah itu, geser anting pada lengan yang menunjukan skala paling besar sampai garis kesetimbangan hampir tercapai.
Jika garis kesetimbangan belum tercapai, geser anting pada lengan yang menunjukan skala lebih kecil sampai garis kesetimbangan tercapai. Dan jika belum juga, lakukan hal yang sama pada anting di lengan selanjutnya sampai titik kesetimbangan benar-benar tercapai.
3. Cara Membaca Skala Hasil Penimbangan
Setelah titik keseimbangan tercapai, selanjutnya Anda tinggal membaca skala hasil penimbangan untuk mengetahui berapa massa benda yang ditimbang. Sebagai contoh, perhatikan gambar di bawah ini!
Pada gambar di atas, dapat kita lihat bahwa lengan pertama menunjukan skala 400 gram, lengan kedua menunjukan skala 50 gram, dan lengan ketiga menunjukan skala 6,5 gram. Dari skala yang ditunjukan ketiga lengan, kita dapat mengetahui massa benda dengan menjumlahkan semua skala yang ditunjukan masing-masing lengan, yaitu 400 gr + 50 gr + 6,5 gr = 456,5 gr.
Untuk mengukur gaya gerak listrik (ggl) dan tegangan jepit kita gunakan alat yang dinamakan Voltmeter. Sedangkan untuk mengukur besar kuat arus, kita gunakan Amperemeter. Berikut ini adalah gambar kedua alat tersebut yang sering digunakan di sekolah-sekolah, fungsi alat ini terdiri dari dua yaitu sebagai pengukur arus (amperemeter) dan sebagai pengukur beda potensial (voltmeter).

Bagaimana cara membaca hasil pengukuran dengan menggunakan amperemeter atau Voltmeter? Sebelum kita membahas mengenai bagaimana cara membaca hasil pengukuran arus listrik dan tegangan, perlu diketahui dulu bagian-bagian dari alat tersebut. Bagian-bagian amperemeter/voltmeter terdiri dari batas ukur, terminal positip skala dan terminal negatip seperti terlihat pada gambar.

Untuk Membaca hasil pengukuran amperemeter/voltmeter kita gunakan rumus:
NP=(PJ/ST) x BU
NP= Nilai pengukuran, PJ = penunjukan jarum, ST=skala tertinggi, dan BU= Batas ukur
NP= Nilai pengukuran, PJ = penunjukan jarum, ST=skala tertinggi, dan BU= Batas ukur
Contoh:
PJ = 20, ST = 50, BU = 25 mA
maka:
NP = (20/50) x 25 mA
= 10 mA
MULTIMETER
Seorang teknisi elektronik biasanya memiliki alat pengukur wajib yang mereka gunakan untuk berbagai keperluan teknis yaitu avometer atau multimeter yang merupakan gabungan dari fungsi alat ukur amperemeter untuk mengukur ampere (kuat arus listrik), voltmeter untuk mengukur volt (besar tegangan listrik) dan ohmmeter untuk mengukur ohm (hambatan listrik).
CONTOH SOAL PEMBAHASAN
Rangkaian sederhana dari hambatan (R) ditunjukkan seperti gambar berikut:

Nilai hambatan R adalah….
A. 1,0 Ω
B. 1,5 Ω
C. 2,0 Ω
D. 2,5 Ω
E. 3,0 Ω
A. 1,0 Ω
B. 1,5 Ω
C. 2,0 Ω
D. 2,5 Ω
E. 3,0 Ω
Pembahasan
Pembacaan Voltmeter
Pembacaan Amperemeter
Besarnya hambatan R adalah
SOAL TUGAS KELAS X MIPA 5 , X MIPA 2
1 Perhatikan gambar berikut.
Jika batas ukur amperemeter 1 A, besar kuat arus yang terukur adalah ....
a. 5 A
b. 10 A
c. 15 A
d. 40 A
e. 50 A
2 Jika voltmeter AC menunjukkan angka 80 dan batas ukur maksimum voltmeter adalah 300 volt maka tegangan hambatan R1 pada saat pengukuran sebesar....

A. 100 volt
B. 150 volt
C. 200 volt
D. 250 volt
E. 300 volt
(Sumber soal : Fisikastudycenter.com-Modifikasi EBTANAS 1989)

A. 100 volt
B. 150 volt
C. 200 volt
D. 250 volt
E. 300 volt
(Sumber soal : Fisikastudycenter.com-Modifikasi EBTANAS 1989)
3 Gambar berikut memperlihatkan pengukuran tegangan listrik pada sebuah hambatan dalam suatu rangkaian.

Jika kuat arus yang mengalir pada rangkaian adalah 2 A, maka nilai tegangan sumber listrik sebesar....
A. 120 volt
B. 180 volt
C. 200 volt
D. 220 volt
E. 240 volt
(Sumber soal : Fisikastudycenter.com)
4 Amperemeter dan Voltmeter digunakan untuk mengukur kuat arus dan tegangan pada suatu rangkaian seperti gambar.

Besar tegangan sumber V adalah.....
A. 3 volt
B. 5 volt
C. 6 volt
D. 10 volt
E. 15 volt
(Sumber soal : Soal UN Fisika 2009 P04)
5. Perhatikan gambar berikut ini.
Jika nilai skala yang ditunjuk jarum adalah 2,4, berapakah hasil pengukuran tersebut?
A. 4,80 A
B. 3,20 A
C. 2,40
D. 0,96 A
E. 0.24 A
6. Dua buah pelat besi diukur menggunakan jangka sorong dan hasilnya adalah seperti gambar berikut!
Berapakah selisih tebal kedua pelat besi tersebut?
A. 0,3 mm
B. 0,6 mm
C. 0,7 mm
D. 0,8 mm
E. 1,7 mm
7. Perhatikan hasil timbangan dengan neraca Ohauss tiga lengan berikut!
Massa benda yang ditimbang adalah ….
A. 546,6 gram
B. 464,5 gram
C. 456,5 gram
D. 364,5 gram
E. 346,5 gram
8.
9.
10. SOAL DIMENSI
Tentukan satuan dan dimensi fluks magnet jika fluks magnet merupakan hasil kali medan magnet dengan luas penampang yang tegak lurus arah medan magnet!
Catatan :
Fluks magnetik
Fluks magnetik
Gambar Fluks magnetik
Fluks magnetik menyatakan jumlah garis gaya yang menembus permukaan dalam arah tegak lurus. Fluks magnetik diperoleh dengan melakukan integrasi dari produk skalar antara vektor medan magnetik dengan vektor elemen luas.

Gambar Fluks magnetik
dan persamaan matematis fluks
Keterangan :
Φ = Fluks magnetik (Wb)
B = Medan magnetik (Wb/m2)
A = Luas penampang (m2)
θ = Sudut antara arah medan magnetik (B) dengan arah normal bidang (N)
TUGAS KELAS XI MIPA 1
MATERI ELASTISITAS
a. Tegangan (δ)
b. Regangan (e)
c. Modulus Elastisitas (Modulus Young )
simbol Y ( Young)
d. Batas Elastis
E
a. Hukum Hooke
b. Tetapan Gaya pada Benda Elastis
c. Hukum Hooke untuk Susunan Pegas
Energi Potensial Pegas
Contoh Soal :
4 Tiang beton mempunyai tinggi 5 meter dan luas penampang lintang 3 m3 menopang beban bermassa 30.000 kg. Hitunglah (a) tegangan tiang (b) regangan tiang (c) perubahan tinggi tiang! Gunakan g = 10 m/s2. Modulus elastis Young Beton = 20 x 109 N/m2
Pembahasan
Diketahui :
Pembahasan
Diketahui :

Ditanya : (a) Tegangan tiang (b) Regangan tiang (c) Perubahan tinggi tiang!
Jawab :
(a) Tegangan tiang
Jawab :
(a) Tegangan tiang

(b) Regangan tiang

(c) Perubahan tinggi tiang

Tiang bertambah pendek 0,025 milimeter.
5. Contoh soal Modulus Young
Sepotong kawat homogen panjangnya 140 cm dan luas penampangnya 2 mm2. Ketika ditarik dengan gaya sebesar 100 N, bertambah panjang 1 mm. Modulus elastik kawat bahan kawat tersebut adalah...
A.7 . 108 N/m2
B.7 . 109 N/m2
C.7 . 1010 N/m2
D.7 . 1011 N/m2
E.7 . 1012 N/m2

6 Contoh soal hukum Hooke
Gambar di bawah menunjukkan grafik hubungan antara gaya (F) dengan pertambahan panjang pegas (∆x).

Dari grafik tersebut konstanta pegas adalah...
A.100 N/m
B.200 N/m
C.300 N/m
D.500 N/m
E.5000 N/m

7
Dalam suatu praktikum untuk menentukan konstanta suatu pegas diperoleh data sebagai berikut:

Jika F adalah gaya dan ∆x adalah pertambahan panjang pegas, maka konstanta pegas yang digunakan adalah...
A.100 N/m
B.200 N/m
C.300 N/m
D.400 N/m
E.500 N/m

8
Suatu pegas akan bertambah panjang 10 cm jika diberi gaya 30 N. Pertambahan panjang pegas jika diberi gaya 21 N adalah...
A.2 cm
B.3 cm
C.5 cm
D.6 cm
E.7 cm

9 Contoh soal energi potensial pegas
Sebuah tali karet diberi beban 300 gram dan digantung vertikal pada sebuah statif. Ternyata karet bertambah panjang 4 cm (g = 10 m/s2). Energi potensial karet tersebut adalah...
A.7,5 . 10-2 joule
B.6,0 . 10-2 joule
C.4,5 . 10-2 joule
D.3,0 . 10-2 joule
E.1,5 . 10-2 joule

10
Contoh soal susunan pegas
Tiga pegas identik dengan konstanta 1000 N/m disusun seperti gambar.

Jika susunan pegas diberi beban sehingga bertambah panjang 6 cm, maka pertambahan panjang masing-masing pegas adalah..


11
Tiga buah pegas disusun seperti gambar dibawah.

Jika konstanta pegas k1 = k2 = 3 N/m dan k3 = 6 N/m, maka konstanta susunan pegas besarnya...
A.1 N/m
B.3 N/m
C.7,5 N/m
D.12 N/m
E.15 N/m

12
Tiga buah pegas identik disusun seperti gambar.

Jika massa beban 300 gram (g = 10 m/s2) digantung pada pegas k1 pegas bertambah panjang 4 cm. Besarnya konstanta susunan pegas adalah...
A.225 N/m
B.75 N/m
C.50 N/m
D.25 N/m
E.5 N/m

13
Tiga pegas identik masing-masing mempunyai konstanta 200 N/m tersusun seri paralel seperti gambar dibawah.

Pada ujung bawah susunan pegas digantungi beban seberat w sehingga susunan pegas bertambah panjang 3 cm. Berat beban w adalah...
A.1 N
B.2 N
C.3 N
D.4 N
E.10 N

SOAL TUGAS XI MIPA 1
1Grafik hubungan antara gaya (F) terhadap penambahan panjang (Δx) suatu pegas ditunjukkan gambar dibawah.

Konstanta pegas yang digunakan adalah...
A.1000 N/m
B.900 N/m
C.800 N/m
D.700 N/m
E.600 N/m
2
Grafik (F-x) menunjukkan hubungan antara gaya dengan pertambahan panjang pegas.

Besar energi potensial pegas berdasarkan grafik di atas adalah...
A.20 joule
B.16 joule
C.3,2 joule
D.1,6 joule
E.1,2 joule
3
Grafik dibawah menunjukkan hubungan antara gaya (F) dengan pertambahan panjang (Δx) sebuah pegas.

Energi potensial pegas pada saat mengalami pertambahan panjang 14 cm adalah...
A.11,2 joule
B.5,6 joule
C.1,12 joule
D.0,56 joule
E.0,112 joule
4

Empat pegas identik masing-masing memiliki konstanta 300 N/m disusun seperti gambar!
Konstanta gabungan keempat pegas adalah...
A.150 N/m
B.225 N/m
C.300 N/m
D.900 N/m
E.1200 N/m
5. Dua kawat A dan kawat B sama panjang dengan perbandingan diameter 5:2, masing-masing ditarik oleh gaya sebesar F, sehingga mengalami pertambahan panjang dengan perbandingn 4:1. Pertanyaannya berapa nilai perbandingan dari modulus young kawat A dan kawat B?
SOAL KELAS XII MIPA 3
Teori Relativitas Newton dan Contoh Soal Serta Pembahasannya
Gerak benda didefinisikan sebagai berubahnya kedudukan suatu benda terhadap titik acuan. Jadi, untuk menyatakan bahwa benda itu bergerak kita harus menentukan suatu titik acuan yang digunakan sebagai patokan. Misalnya, Iwan dan Eka pergi ke Surabaya dengan naik kereta api, menurut pengamat yang berdiri diam di stasiun mengatakan Iwan itu bergerak, sedangkan menurut Eka yang duduk di samping Iwan di dalam kereta itu mengatakan Iwan itu diam tidak bergerak. Jadi dalam hal ini Iwan dapat dikatakan diam atau bergerak tergantung pada titik acuan yang dipakai. Apabila kerangka acuan adalah stasiun, dikatakan Iwan bergerak. Akan tetapi, jika kerangka acuan yang digunakan adalah Eka yang duduk disamping Iwan di dalam kereta api, maka Iwan itu dikatakan diam.
Jadi, benda yang bergerak itu bersifat relatif, yaitu tergantung pada kerangka acuan yang digunakan. Berdasarkan contoh peritiwa di atas maka kerangka acuan dapat dibedakan menjadi dua yakni kerangka acuan yang diam dan kerangka acuan yang bergerak. Gerak benda yang bersifat relatif dikenal dengan teori relativitas.
Teori Relativitas sudah dikenal sejak jamannya Newton. Pada relativitas Newton, semua besaran akan sama saat diukur oleh pengamat yang diam maupun pengamat yang bergerak. Besaran yang berubah hanyalah kecepatan relatif dan berlaku persamaan sebagai berikut.
vx’ = v - vx
dengan:
vx’ = kecepatan relatif benda terhadap pengamat bergerak
vx = kecepatan relatif benda terhadap pengamat diam
v = kecepatan pengamat bergerak terhadap pengamat diam
Dalam fisika modern penjumlahan kecepatan menurut teori Relativitas Newton dikenal dengan istilah transformasi Galileo. Untuk memantapkan pemahaman Anda tentang teori relatifitas Newton silahkan pelajari contoh soal di bawah ini dan silahkan coba jawab soal latihannya.
Contoh Soal 1
Sebuah kereta api bergerak dengan kecepatan 120 km/jam. Pada saat itu Salim berlari di atas kereta dengan kecepatan 10 km/jam searah kereta. Berapakah kecepatan Salim tersebut menurut orang yang berada di dalam kereta api dan orang yang berdiri di stasiun?
Penyelesaian:
Stasiun relatif diam menjadi kerangka acuan terhadap kereta api dan kereta api sebagai kerangka acuan terhadap Salim. Maka kecepatan Salim relatif terhadap kereta api adalah:
vx’ = +10 km/jam
Sedangkan kecepatan Salim terhadap stasiun adalah vx, besarnya memenuhi:
vx = v + vx’
vx = 120 + 10
vx = 130 km/jam
Soal Latihan
Perhatikan gambar di bawah ini.
 |
| Pesawat tempur Sumber: wikipedia |
Sebuah pesawat perang terbang meninggalkan bumi dengan kecepatan 1200 km/jam. Pada saat itu pesawat melepaskan rudal dengan kecepatan 200 km/jam searah pesawat. Berapakah kecepatan rudal tersebut menurut orang yang berada di bandara lepas landas pesawat tersebut?
Nah itu contoh kasus gerak yang kecepatannya di bawah kecepatan cahaya, bagaimana dengan jika kecepatan sebuah benda atau partikel yang mendekati kecepatan cahaya (c) seperti contoh soal di bawah ini.
Contoh Soal 2
Partikel B bergerak terhadap A dengan kecepatan 0,8c ke kanan. Partikel C bergerak terhadap B dengan kecepatan 0,6c ke kanan. Tentukan kecepatan partikel C relatif terhadap A berdasarkan relativitas Newton.
Penyelesaian:
Partikel A diam menjadi kerangka acuan dari partikel B dan partikel B sebagai kerangka acuan dari partikel C. Maka kecepatan partikel C relatif terhadap A yakni:
vx = v + vx’
vx = 0,8c + 0,6c
vx = 1,4c
Jadi, kecepatan partikel C relatif terhadap A adalah 1,4c.
Kita ketahui bahwa tidak ada sebuah partikel yang mampu bergerak melebihi kecepatan cahaya (c), sehingga rumus perhitungan teori relativitas newton seperti contoh soal 2 di atas tidak berlaku lagi. Oleh karena itu, untuk gerak partikel yang memiliki kecepatan mendekati kecepatan cahaya maka penjumlahan kecepatannya dapat menggunakan teori relativitas Einstein.
MATERI & CONTOH SOAL RELATIVITAS EINSTEN
RANGKUMAN RUMUS
Teori gelombang Huygens telah membuat masalah yang harus memperoleh penyelesaian, yakni tentang medium yang merambatkan cahaya. Lazim disebut eter.
Pada tahun 1887 Michelson dan Morley mengadakan percobaan-percobaan yang sangat cermat, hasilnya sangat mengejutkan, karena adanya eter tidak dapat dibuktikan dengan percobaan.
Hasil percobaan Michelson dan Morley mencakup dua hal yang penting.
- Hipotesa tentang medium eter tidak dapat diterima sebagai teori yang benar, sebab medium eter tidak lulus dari ujian pengamatan.
- Kecepatan cahaya adalah sama dalam segala arah, tidak bergantung kepada gerak bumi.
Di atas telah dibahas bahwa kecepatan cahaya ke segala arah adalah sama, tidak bergantung pada gerak bumi. Tetapi bumi bukanlah satu-satunya planet yang ada dalam jagad raya ini. Kalau begitu bagaimana kecepatan cahaya itu ditinjau dari planet lain yang geraknya berbeda dengan gerakan bumi.
Pada tahun 1905, Einstein mengusulkan bahwa kecepatan cahaya yang besarnya sama ke segala arah itu berlaku ditempat-tempat lain dalam alam semesta ini. Tegasnya kecepatan cahaya adalah sama, tidak bergantung kepada gerak sumber cahaya maupun pengamatnya.
Teori Einstein membawa akibat-akibat yang sangat luas dirasakan agak menyimpang dari pengalaman-pengalaman yang kita peroleh sehari-hari.
Teori Relativitas Einsten (untuk kecepatan tinggi / dalam satuan c / mendekati kecepatan cahaya)
Teori Relativitas Einsten (untuk kecepatan tinggi / dalam satuan c / mendekati kecepatan cahaya)
Relativitas penjumlahan kecepatan.
Bila v1 adalah laju kereta api terhadap tanah, dan v2 adalah laju orang terhadap kereta api, maka laju orang terhadap tanah :
c adalah kecepatan cahaya
Teori relativitas Einstein memperkirakan adanya efek-efek ganjil ketika suatu benda mendekati kecepatan cahaya. Teori relativitas Einstein ini mempertimbangkan konsep kerangka acuan inersia. Teori hipotesis eter telah membuktikan secara tidak langsung bahwa eter itu tidak ada. Albert Einstein pada tahun 1905 mengusulkan teori relativitas khusus.
Teori Relativitas Einstein
Teori ini bertolak pada kerangka acuan inersial yaitu kerangka acuan yang bergerak relatif dengan kecepatan konstan terhadap kerangka acuan yang lain. Sepuluh tahun kemudian pada tahun 1915, Einstein mengemukakan teori relativitas umum yang bertolak dari kerangka acuan yang bergerak dipercepat terhadap kerangka acuan yang lainnya.
Postulat Teori Relativitas Einstain
Dalam mengemukakan teori relativitas khusus ini Einstein mengemukakan dua postulat, kedua postulat tersebut kemudian menjadi dasar teori relativitas khusus. Kedua postulat itu adalah :
- Postulat pertama, hukum fisika dapat dinyatakan dalam persamaan yang berbentuk sama dalam semua kerangka acuan inersia.
- Postulat kedua, kecepatan cahaya dalam ruang hampa sama besar untuk semua pengamat, tidak tergantung dari keadaan gerak pengamat itu. Kecepatan cahaya di ruang hampa sebesar c = 3.108 m/s.
Dengan dasar dua postulat tersebut dan dibantu secara matematis dengan transformasi Lorentz, Einstain dapat menjelaskan relativitas khusus dengan baik. Hal terpenting yang perlu dijelaskan dalam transformasi Lorentz adalah semua besaran yang terukur oleh pengamat diam dan bergerak tidaklah sama kecuali kecepatan cahaya. Besaran -besaran yang berbeda itu dapat dijelaskan seperti dibawah.
Pada postulat yang pertama tersebut menyatakan ketiadaan kerangka acuan universal. Apabila hukum fisika berbeda untuk pengamat yang berbeda dalam keadaan gerak relatif, maka kita dapat menentukan mana yang dalam keadaan “diam” dan mana yang “bergerak” dari perbedaan tersebut. Akan tetapi karena tidak ada kerangka acuan universal, perbedaan itu tidak terdapat, sehingga muncullah postulat ini. Postulat pertama menekankan bahwa prinsip Relativitas Newton berlaku untuk semua rumus Fisika, tidak hanya dalam bidang mekanika, tetapi pada hukum-hukum Fisika lainnya. Sedangkan postulat yang kedua sebagai konsekuensi dari postulat yang pertama, sehingga kelihatannya postulat kedua ini bertentangan dengan teori Relativitas Newton dan transformasi Galileo tidak berlaku untuk cahaya. Dalam postulat ini Einstein menyatakan bahwa selang waktu pengamatan antara pengamat yang diam dengan pengamat yang bergerak relatif terhadap kejadian yang diamati tidak sama (t ≠ t’). Menurut Einstein besaran kecepatan, waktu, massa, panjang adalah bersifat relatif. Untuk dapat memasukkan konsep relativitas Einstein diperlukan transformasi lain, yaitu transformasi Lorentz.
Akibat Postulat Einstain
Pada postulat Einstain telah dijalaskan bahwa besaran yang tetap dan sama untuk semua pengamat hanyalah kecepatan cahaya berarti besaran lain tidaklah sama. Besaran – besaran itu diantaranya adalah kecepatan relatih benda, panjang benda waktu, massa dan energi.
a. Kecepatan relatif
Jika ada sebuah pesawat (acuan O’) yang bergerak dengan kecepatan v terhadap bumi (acuan O) dan pesawat melepaskan bom (benda) dengan kecepatan tertentu maka kecepatan bom tidaklah sama menurut orang di bumi dengan orang di pesawat. Kecepatan relatif itu memenuhi persamaan berikut.
dengan :
vx = kecepatan benda relatif terhadap pengamat diam (m/s)
vx’ = kecepatan benda relatif terhadap pengamat bergerak (m/s)
v = kecepatan pengamat bergerak (O’) relatif terhadap pengamat diam (O)
c = kecepatan cahaya
vx’ = kecepatan benda relatif terhadap pengamat bergerak (m/s)
v = kecepatan pengamat bergerak (O’) relatif terhadap pengamat diam (O)
c = kecepatan cahaya
b. Kontransi Panjang
Kontransi panjang adalah penyusutan panjang suatu benda menurut pengamat yang bergerak. Penyusutan ini memenuhi persamaan berikut.
dengan :
L = panjang benda menurut pengamat yang bergerak relatif terhadap benda
L0 = panjang benda menurut pengamat yang diam relatif terhadap benda
L0 = panjang benda menurut pengamat yang diam relatif terhadap benda
c. Dilatasi Waktu
Dilatasi waktu adalah peristiwa pengembungan waktu menurut pengamat yang bergerak. Hubungannya memenuhi persamaan berikut.
dengan :
Δt = selang waktu menurut pengamat yang bergerak terhadap kejadian
Δt0 = selang waktu menurut pengamat yang diam terhadap kejadian
Δt0 = selang waktu menurut pengamat yang diam terhadap kejadian
d. Massa dan energi relatif
Perubahan besaran oleh pengamat diam dan bergerak juga terjadi pada massa benda dan energinya.
Dan energi benda diam dan bergerak memiliki hubungan sebagai berikut.
(a) Energi total : E = mc2
(b) Energi diam : E0 = m0 c2
(c) Energi kinetik : Ek = E – E0
(b) Energi diam : E0 = m0 c2
(c) Energi kinetik : Ek = E – E0
Poin-poin diatas merupakan formulasi energi dari teori relativitas einstein.
MATERI RELATIVITAS KHUSUS
KECEPATAN RELATIVISTIK

Keterangan:
vA = kecepatan benda A.
vB = kecepatan benda B.
vAB = kecepatan benda A terhadap benda B.
c = kecepatan cahaya.
KONTRAKSI PANJANG

DILATASI WAKTU

MASSA RELATIVISTIK

Contoh Soal Penjumlahan Kecepatan Berdasarkan Relativitas Einstein (1)
Jawab:
Contoh Soal Penjumlahan Kecepatan Berdasarkan Relativitas Einstein (2)
Jawab:
Contoh Soal Penjumlahan Kecepatan Berdasarkan Relativitas Einstein (1)
Pesawat angkasa P berkecepatan 0,9 c terhadap bumi. Apabila pesawat angkasa Q bergerak melewati pesawat P dengan kecepatan relatif 0,5 c terhadap pesawat P, berapakah kecepatan pesawat Q terhadap bumi?
Jawab:
Pesawat Q memerlukan kecepatan relatif terhadap bumi adalah 0,9 + 0,5 c = 1,4 c, jelas tidak mungkin. Akan tetapi, menurut persamaan relativitas dengan u’x = 0,5 c, v = 0,9 c, kecepatan relatif yang diperlukan adalah:
Contoh Soal Penjumlahan Kecepatan Berdasarkan Relativitas Einstein (2)
Dua pesawat A dan B bergerak dalam arah yang berlawanan. Kelajuan pesawat A sebesar 0,5 c dan kelajuan pesawat B adalah 0,4 c. Tentukanlah kelajuan pesawat A relatif terhadap B.
Jawab:
Kita mencoba tentukan arah kanan sebagai arah positif, B bergerak ke arah kiri. Berdasarkan relativitas Einstein
Kaji-1: Menurut pengamat disebuah planet ada dua pesawat antariksa yang mendekatinya dari arah yang berlawanan, masing-masing pesawat A yang kecepatannya 0.5c dan pesawat B yang kecepatannya 0.4c. Menurut pilot pesawat A, tentukanlah besar kecepatan pesawat B!
Jawab:
Besaran yang diketahui.
Lihat sketsa peristiwa di bawah ini.
Kecepatan pesawat B menurut A adalah

Latih-1: Menurut pengamat disebuah planet ada dua pesawat antariksa yang mendekatinya dari arah yang berlawanan, masing-masing pesawat A yang kecepatannya 0.5c dan pesawat B yang kecepatannya 0.5c. Menurut pilot pesawat A, tentukanlah besar kecepatan pesawat B!
Kaji-2: Sebuah atom bergerak dengan kecepatan 0.3c terhadap laboratorium, memancarkan elektron pada arah yang sama dengan laju 0.6c terhadap atom. Tentukanlah kelajuan elektron menurut pengamat dilaboratorium!
Jawab:
Besaran yang diketahui.

A menunjukkan identitas atom, L menunjukkan identitas laboratorium, dan E menunjukkan identitas elektron. Jadi kelajuan elektron terhadap pengamat laboratorium adalah

Latih-2: Sebuah atom bergerak dengan kecepatan 0.4c terhadap laboratorium, memancarkan elektron pada arah yang sama dengan laju 0.8c terhadap atom. Tentukanlah kelajuan elektron menurut pengamat dilaboratorium!
Kaji-3: Dua buah roket A dan B mendekati bumi dengan kelajuan relative terhadap bumi adalah sama. Tentukanlah kelajuan masing-masing roket tersebut jika kelajuan relatif satu terhadap yang lainnya adalah 0.5c!
Jawab:
Besaran yang diketahui.

Kelajuan masing-masing roket terhadap bumi adalah


Kaji-1: Menurut pengamat disebuah planet ada dua pesawat antariksa yang mendekatinya dari arah yang berlawanan, masing-masing pesawat A yang kecepatannya 0.5c dan pesawat B yang kecepatannya 0.4c. Menurut pilot pesawat A, tentukanlah besar kecepatan pesawat B!
Jawab:
Besaran yang diketahui.
Kecepatan pesawat B menurut A adalah

Latih-1: Menurut pengamat disebuah planet ada dua pesawat antariksa yang mendekatinya dari arah yang berlawanan, masing-masing pesawat A yang kecepatannya 0.5c dan pesawat B yang kecepatannya 0.5c. Menurut pilot pesawat A, tentukanlah besar kecepatan pesawat B!
Jawab:
Besaran yang diketahui.
A menunjukkan identitas atom, L menunjukkan identitas laboratorium, dan E menunjukkan identitas elektron. Jadi kelajuan elektron terhadap pengamat laboratorium adalah

Latih-2: Sebuah atom bergerak dengan kecepatan 0.4c terhadap laboratorium, memancarkan elektron pada arah yang sama dengan laju 0.8c terhadap atom. Tentukanlah kelajuan elektron menurut pengamat dilaboratorium!
Jawab:
Besaran yang diketahui.
Kelajuan masing-masing roket terhadap bumi adalah

CONTOH SOAL RELATIVITAS KHUSUS DAN PEMBAHASAN
Nomor 1
Seorang pengamat di stasiun ruang angkasa mengamati adanya dua pesawat antariksa A dan B yang datang menuju stasiun tersebut dari arah yang berlawanan dengan laju vA = 4/5 c dan vB = 5/6 c (c adalah cepat rambat cahaya). Kelajuan pesawat B menurut pilot pesawat A adalah…
A. 11/9 c
B. 49/50 c
C. 24/25 c
D. 9/11 c
E. 2/3 c
Nomor 2
Seorang pengamat di stasiun ruang angkasa mengamati adanya dua pesawat antariksa A dan B yang datang menuju stasiun tersebut dari arah yang berlawanan dengan laju vA = 4/5 c dan vB = 5/6 c (c adalah cepat rambat cahaya). Kelajuan pesawat B menurut pilot pesawat A adalah…
A. 11/9 c
B. 49/50 c
C. 24/25 c
D. 9/11 c
E. 2/3 c
Nomor 2
Dua benda bergerak dengan kecepatan masing-masing ½ c dan ¼ c arah berlawanan. Bila c = kecepatan cahaya, maka kecepatan benda pertama terhadap benda kedua sebesar...
A. 0,125 c
B. 0,250 c
C. 0,500 c
D. 0,666 c
E. 0,750 c
Nomor 3
A. 0,125 c
B. 0,250 c
C. 0,500 c
D. 0,666 c
E. 0,750 c
Nomor 3
Roket yang sedang diam panjangnya 10 m. Jika roket itu bergerak dengan kecepatan 0,8 c (c = kecepatan cahaya = 3 x 108 m.s-1), maka menurut pengamat di bumi panjang roket tersebut selama bergerak adalah....
A. 5 m
B. 6 m
C. 7 m
D. 8 m
E. 9 m
Nomor 4
A. 5 m
B. 6 m
C. 7 m
D. 8 m
E. 9 m
Nomor 4
Balok dalam keadaan diam panjangnya 2 meter. Panjang balok menurut pengamat yang bergerak terhadap balok dengan kecepatan 0,8 c ( c = laju cahaya) adalah....
A. 0,7 m
B. 1,2 m
C. 1,3 m
D. 1,6 m
E. 2,0 m
Nomor 5
A. 0,7 m
B. 1,2 m
C. 1,3 m
D. 1,6 m
E. 2,0 m
Nomor 5
Sebuah pesawat antariksa melewati bumi dengan kelajuan 0,6 c. Menurut penumpang pesawat panjang pesawat L, maka menrut orang dibumi panjang pesawat adalah...
A. 2L
B. L
C. 0,8 L
D. 0,6 L
E. 0,4 L
A. 2L
B. L
C. 0,8 L
D. 0,6 L
E. 0,4 L
Seseorang yang bergerak dengan laju 0,8 c melihat orang yang memungut sebuah jam. Menurut pengamatannya orang itu memungut jam dalam tempo 10 detik. Berapa lama waktu itu dirasakan oleh orang yang memungut jam ?
Nomor 7
Sebuah benda dalam keadaan diam massanya 1 kg. Berapakah massa benda itu jika bergerak dengan kecepatan 0,4 c ?
Nomor 8
Hitunglah kecepatan sebuah partikel yang mempunyai energi kinetik 5/3 energi diamnya.















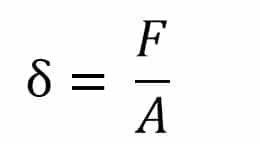
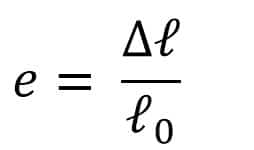
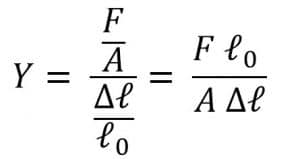
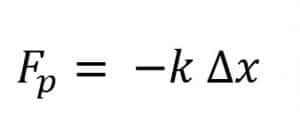
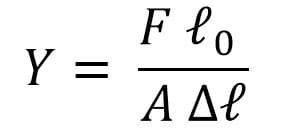
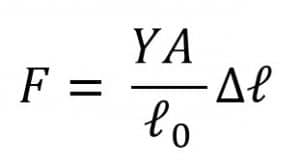
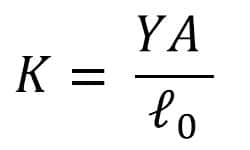
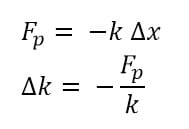
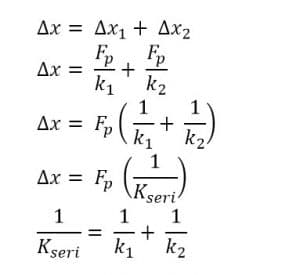
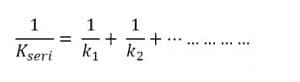

.jpg)
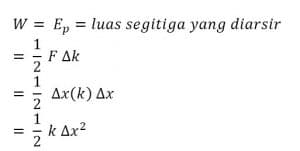
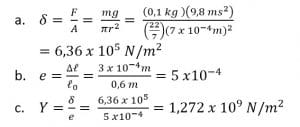
















No comments:
Post a Comment